Valve Flow Coefficients
Most solenoid valves, coaxial valves, pneumatic valves, process control solenoid or mechanical valve, angle seat piston or any process valve supplied will give a media flow factor or flow coefficient advising the expected flow through the valve under certain parameters which allows customers to correctly size the valve to meet the needs of the application in hand. Installing a valve under specification will mean insufficient flow, and over specification may lead to water hammer or just simply excess cost.
What is a valve Kv value?
The Kv value or flow coefficient of the valve is typically based on the expected flow of water through the valve with a pressure drop or pressure difference of 1 bar, So, for example a PU220A-04 1/2" BSP Brass 2/2 normally closed Shako solenoid valve with a Kv flow factor of 35 will flow 35 litres a minute with a 1 bar inlet pressure and a outlet pressure of zero or to atmosphere i.e. pressure difference of 1 bar. The same is true for the same valve with a 4 bar inlet and a 3 bar outlet pressure, as this gives the same 1 bar pressure difference or differential. More flow can be achieved by increasing the pressure difference and this can easily be calculated by a simple fluid flow formulae below:
Kv Flow Formula.
Flow in litres a minute = Kv valve flow factor multiplied by the square root of pressure drop x density of the media.
Example of Calculating flow of water using Kv value.
What flow will I get with a PU220A-04 solenoid valve with 3 bar inlet, outlet open to tank.
Pressure difference is inlet 3 bar minus outlet 0 = ΔP is 3 bar. (ΔP Delta P is pressure differential)
Therefore, expected flow in litres a minute = Kv valve value 35 x √(pressure drop = 3 bar divided by density of water, which is 1).
Expected Flow = 35 x √(3 divided by 1)
Expected flow = 35 x √3
Expected flow = 35 x 1.732
Flow = 60.62 litres a minute.
So we know our expected flow of water with 3 bar inlet and outlet open-ended would be 60.62 litres a minute
Example of Calculating Pressure Drop across a Valve.
We need to rearrange the Kv liquid flow formula, as the ΔP Delta P pressure differential is the unknown factor.
ΔP Delta P = d density of media x (Q flow / Kv flow factor)2
Example: What would be the pressure drop of a Shako PU220A-08 1" BSP solenoid valve with a Kv factor of 183 for a flow of 200 litres a minute on a mains water inlet pressure of 4 bar.
ΔP Delta P = d density of media x (Q flow / Kv flow factor)2
ΔP Delta P = d density of water (1) x (Q flow 200 / Kv flow factor which is 183)2
ΔP = 1 x (200 divided by 183)2
ΔP = 1 x (1.092896)2
ΔP = 1 x 1.19442
So a Shako PU220A-08 solenoid valve with Kv factor of 183 with 4 bar water pressure and 200 litres a minute flow will have a pressure drop of 1.19442 Bar, which means at this flow and pressure the outlet pressure will have dropped from 4 bar (less ΔP of 1.19442) to 2.8 Bar.
Choosing the correct size of solenoid valve.
One of the biggest headaches for engineers or valve users to knowing what size of valve to use. If the valve is too small then there will be insufficient flow and if the valve is too big and requires a minimum pressure difference to operate it may not work or at least just be more expensive. So long as you know the inlet pressure, media viscosity, flow required then it is quite easy to calculate the valve Kv flow coefficient required.
For a simple example we want a water solenoid valve to flow 500 litres a minute at 10 bar, and we need a minimum pressure drop of 0.5 bar as the valve needs to be pressure assisted.
Knowing that Kv factors are based on 1 bar pressure drop, we can use this as guidance that a valve with a Kv flow factor of 500 will flow 500 litres of water with a pressure drop of 1 bar, which meets the minimum 0.5 bar pressure drop required.
Looking at the Shako PU225A series solenoid valves, the PU225A-12 11/2" BSP solenoid valve has a Kv value of 500 exactly, so this would be a good starting point.
Choosing two sizes down to 1" valve with a Kv value of 165 would mean a pressure drop of
ΔP Delta P = d density of media x (Q flow / Kv flow factor)2
ΔP = 1 x (500 / 165)2
ΔP = 1x 3.032 = 9 Bar, so this pressure drop is far too high, inlet 10 bar ΔP 9 bar means outlet pressure 1 bar to achieve this flow.
Helpful Hint: when choosing a solenoid valve, try to stay under a 10% pressure drop.
Choosing the next size up to a 2" valve with a Kv value of 600 would mean a pressure drop of
ΔP Delta P = d density of media x (Q flow / Kv flow factor)2
ΔP = 1 x (500 / 600)2
ΔP = 1 x (0.83)2
ΔP = 0.69 Bar.
We can deduce from these figures that a solenoid valve for water at 10 bar for 500 litres a minute that an 11/2" valve ΔP of 1 Bar and a 2" valve ΔP of 0.69 Bar would both work well. Choice would be down to valve cost and current pipe sizes, so if you already have 11/2" pipe then use 11/2 valve, if you have a 2" pipe buying reducing bushes and fitting them to use a smaller valve may prove costly and time and space consuming.
Helpful Hint: If you are not sure how to size your valve to your application, contact a good valve supplier who can calculate the best option for you.
Definitions and conversion factors for the three valve flow coefficients Kv, Cv and Qn.
1. What is the Kv Value
Kv value is the metric measure for the flow of a valve. It is defined as:
The volume flow in cubic metres per hour of water at a temperature of between 5° and 40° Celsius, with a pressure drop across the valve of 1 bar.
2. What is the Cv Value?
Cv is the imperial measure for the flow of a valve. It is defined as:
The volume flow in US gallons per minute of water at a temperature of 60° Fahrenheit with a pressure drop across the valve of 1 psi.
3. What is the Qn Value?
Qn value is used in pneumatics to define the flow of a valve. It is defined as:
The volume flow in litres per minute of air at a temperature of 20° Celsius, with an input pressure of 6 bar and a pressure drop across the valve of 1 bar.
4. Converting between Kv and Cv
Kv = 0.86 x Cv
Converting between Kv and Qn
Kv = Qn / 1078
Converting between Cv andKv
Cv = Kv / 0.86
Converting between Cv and Qn
Cv = Qn x 0.0008
Converting between Qn and Kv
Qn = Kv x 1078
Converting between Qn and Cv
Qn = Cv / 0.0008
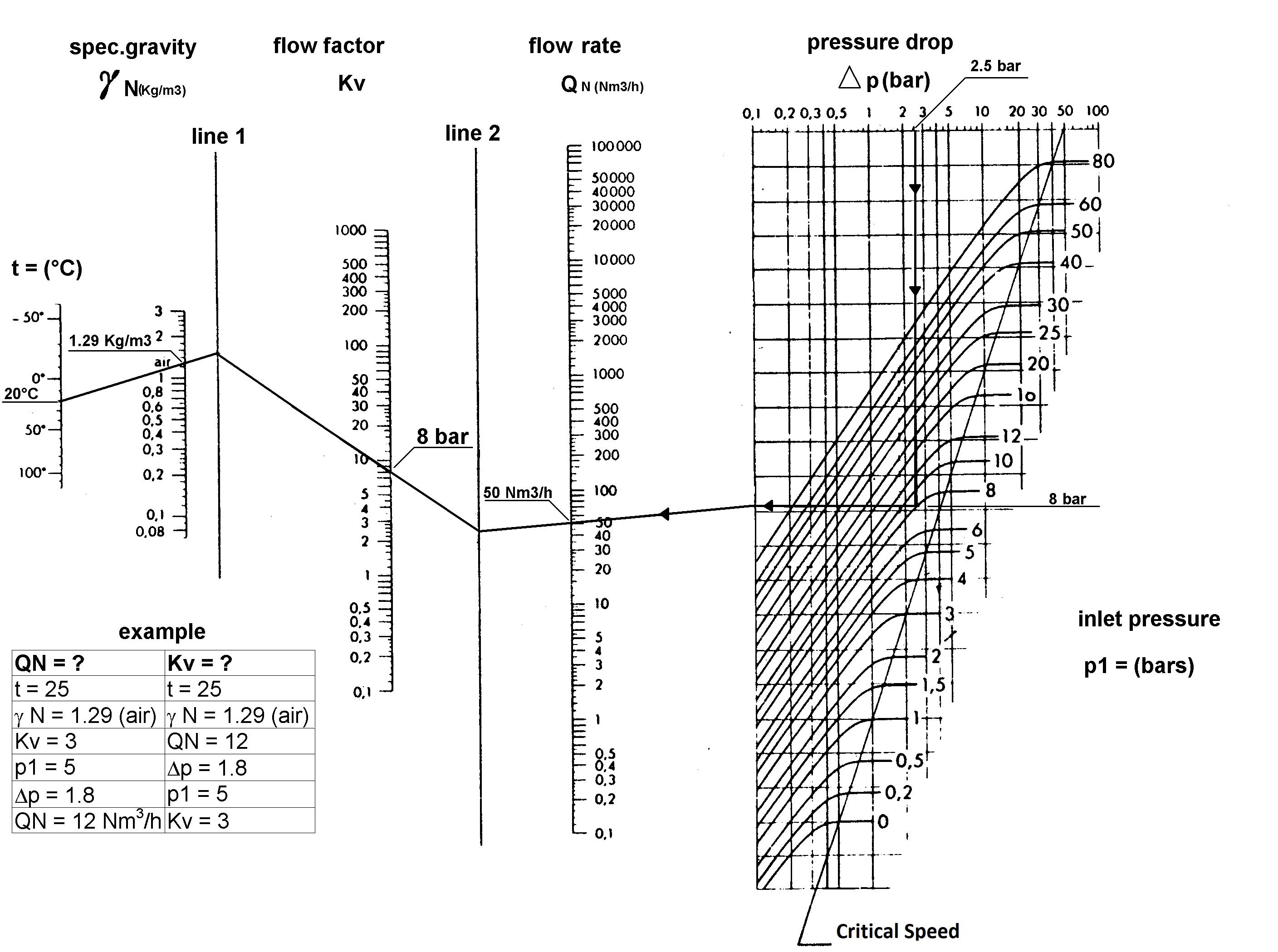
FLOW CHART FOR GASES
How to calculate the flow rate of a gas through a solenoid valve (example) :
How to calculate the flow coefficient (Kv) of a solenoid valve to obtain an air flow at 20°C of 50 Nm3/h with 7 bar pressure (i.e 8 bar relative pressure), a pressure drop (ΔP) of 2.5 bar, and a specific gravity of 1.29, using the graph below.
1. Draw a vertical straight line from the value 2.5 on the Dp axis down to the pressure curve (p1) of 8 bar. Then horizontally transfer this break point to the vertical line of ΔP= 0.1.
2. Draw a straight line from this new break point up to the point 50 on the flow rate axis, and prolong it up to the mark line no 2.
3. Draw a straight line intersecting the values 20 and 1.29 on the axis of temperature and specific gravity. Prolong this line up to the mark line no 1.
4. Draw a straight line between the break points of mark lines no1 and 2. This line intersects the Kv axis and gives you the value you were looking for : 8l/mn
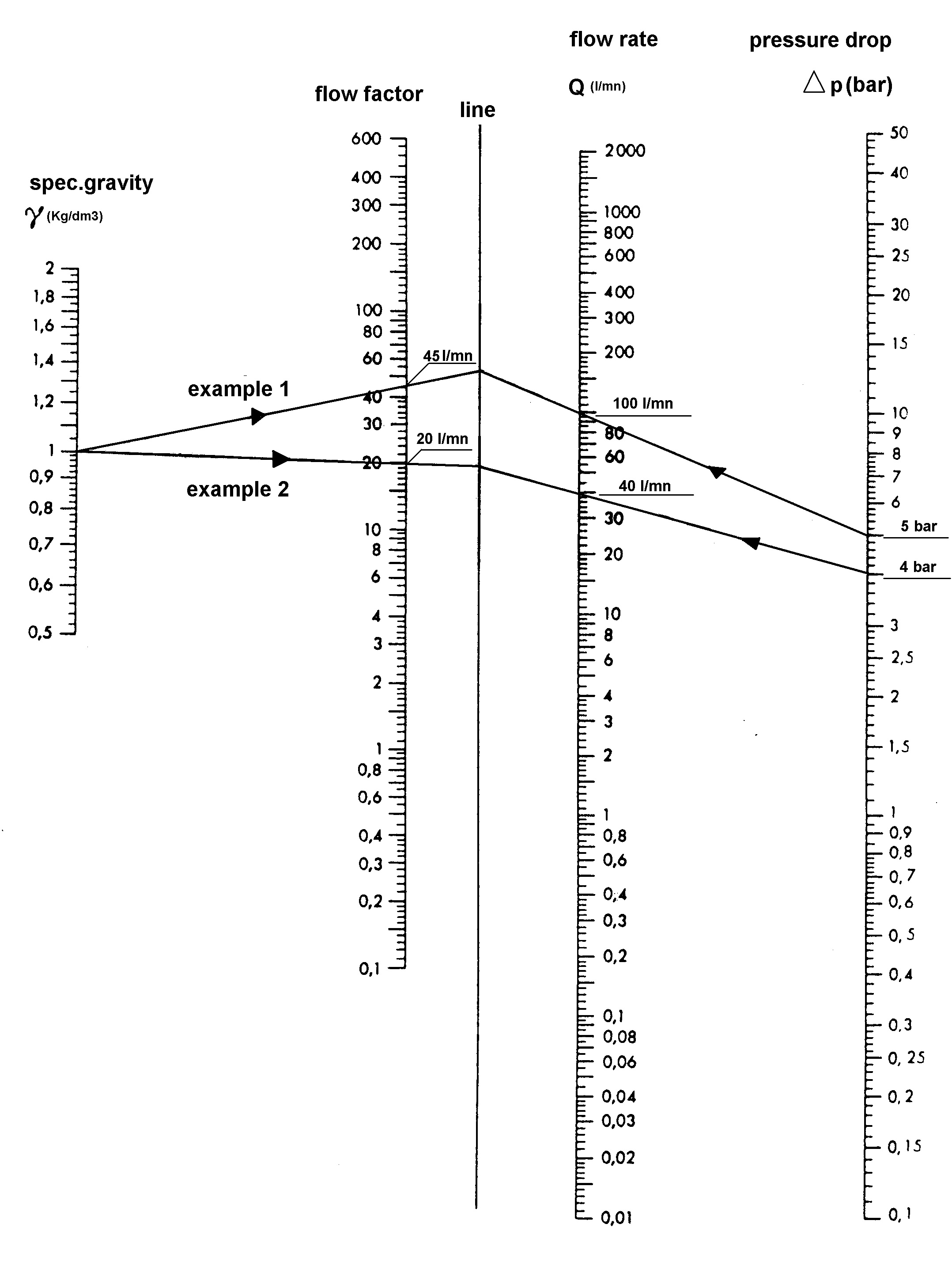
Flow Chart for Liquids and Fluids
How to calculate the flow rate of a fluid or liquid through a solenoid valve.
Example 1: calculate the flow coefficient (Kv) of a solenoid valve to obtain a water flow of 100 l/mn with 5 bar pressure drop. Specific gravity of water=1kg/dm3
1. Draw a straight line intersecting the values 5 and 100 on the axis of pressure drop and flow rate.
2. Prolong this line up to the mark line.
3. Draw a straight line intersecting value 1 on the axis of specific gravity up to the break point of the first straight line with the mark line.
4. This line intersects the Kv axis and gives you the value you were looking for : 45 l/mn
Example 2: Calculate the flow coefficient (Kv) of a solenoid valve to obtain a water flow of 20 l/mn with 4 bar pressure drop. Specific gravity of water=1kg/dm3
a. Draw a straight line intersecting the values 1 and 20 on the axis of specific gravity and Kv.
b. Prolong this line up to the mark line.
c. Draw a straight line intersecting the value 4 on the axis of pressure drop and the break point of the first straight line with the mark line.
d. This line intersects the axis of flow rate and gives you the value you were looking for : 40 l/mn